Mastering Algebra 1: A Comprehensive Textbook Guide
Getting Started with Algebra 1

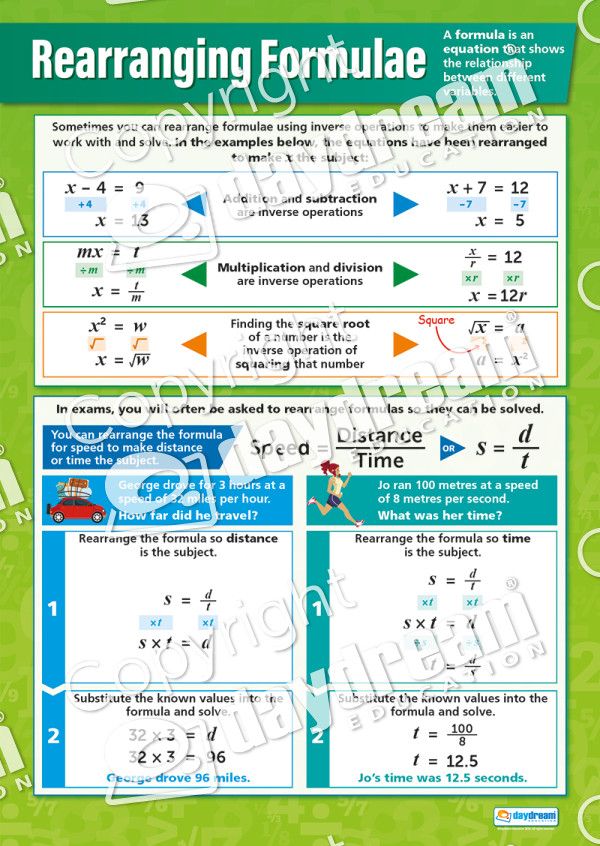
Algebra 1 is a fundamental course in mathematics that builds upon the concepts learned in elementary and middle school. It is a crucial subject that introduces students to variables, equations, and functions, which are essential for problem-solving in various fields, including science, technology, engineering, and mathematics (STEM). In this comprehensive guide, we will walk you through the key concepts, formulas, and techniques to master Algebra 1.
Understanding Variables and Expressions

Variables are letters or symbols that represent unknown values or quantities. In Algebra 1, you will learn how to work with variables, constants, and mathematical operations to simplify expressions and solve equations.
- Variables: Represent unknown values or quantities, e.g., x, y, or z.
- Constants: Represent fixed values, e.g., 2, 5, or 10.
- Mathematical Operations: Include addition, subtraction, multiplication, and division.
To simplify expressions, you need to apply the order of operations (PEMDAS):
- Parentheses: Evaluate expressions inside parentheses first.
- Exponents: Evaluate any exponential expressions next.
- Multiplication and Division: Evaluate multiplication and division operations from left to right.
- Addition and Subtraction: Finally, evaluate any addition and subtraction operations from left to right.
Examples of Simplifying Expressions

| Expression | Simplified Expression |
|---|---|
| 2x + 5 - 3 | 2x + 2 |
| 4(2 + 3) | 4(5) = 20 |
| x^2 + 2x - 3 | x^2 + 2x - 3 (cannot be simplified further) |
Linear Equations and Inequalities

Linear equations are equations in which the highest power of the variable(s) is 1. In Algebra 1, you will learn how to solve linear equations and inequalities using various methods.
- Linear Equations: Equations in which the highest power of the variable(s) is 1, e.g., 2x + 3 = 5.
- Linear Inequalities: Inequalities in which the highest power of the variable(s) is 1, e.g., 2x + 3 > 5.
To solve linear equations, you can use:
- Addition and Subtraction: Add or subtract the same value to both sides of the equation to isolate the variable.
- Multiplication and Division: Multiply or divide both sides of the equation by the same non-zero value to isolate the variable.
Examples of Solving Linear Equations

| Equation | Solution |
|---|---|
| 2x + 3 = 5 | x = 1 |
| x - 2 = 3 | x = 5 |
| 4x = 12 | x = 3 |
Graphing Linear Equations

Graphing linear equations is a visual representation of the equation on a coordinate plane. In Algebra 1, you will learn how to graph linear equations using the slope-intercept form (y = mx + b), where:
- m: Represents the slope of the line.
- b: Represents the y-intercept of the line.
To graph a linear equation, you can use:
- Table of Values: Create a table of values to plot points on the coordinate plane.
- Slope-Intercept Form: Use the slope-intercept form to graph the line.
Example of Graphing a Linear Equation

| Equation | Graph |
|---|---|
| y = 2x + 1 | A line with a slope of 2 and a y-intercept of 1 |
📝 Note: Graphing linear equations is an essential concept in Algebra 1, as it helps visualize the relationship between the variables.
Systems of Linear Equations

Systems of linear equations are sets of two or more linear equations that have the same variables. In Algebra 1, you will learn how to solve systems of linear equations using various methods.
- Substitution Method: Substitute one equation into the other equation to solve for one variable.
- Elimination Method: Add or subtract the equations to eliminate one variable.
Example of Solving a System of Linear Equations

| Equations | Solution |
|---|---|
| 2x + 3 = 5, x - 2 = 3 | x = 1, y = 3 |
| x + 2 = 4, 3x - 2 = 5 | x = 2, y = 1 |
Functions

Functions are relations between variables in which each input corresponds to exactly one output. In Algebra 1, you will learn how to work with functions, including:
- Domain: The set of all input values.
- Range: The set of all output values.
- Function Notation: Use function notation to represent functions, e.g., f(x) = 2x + 1.
Example of a Function

| Function | Domain | Range |
|---|---|---|
| f(x) = 2x + 1 | All real numbers | All real numbers |
📝 Note: Functions are a fundamental concept in Algebra 1, as they help model real-world relationships between variables.
Quadratic Equations and Functions

Quadratic equations are equations in which the highest power of the variable(s) is 2. In Algebra 1, you will learn how to solve quadratic equations and work with quadratic functions.
- Quadratic Equations: Equations in which the highest power of the variable(s) is 2, e.g., x^2 + 2x + 1 = 0.
- Quadratic Functions: Functions in which the highest power of the variable(s) is 2, e.g., f(x) = x^2 + 2x + 1.
To solve quadratic equations, you can use:
- Factoring: Factor the quadratic expression to solve for the variable.
- Quadratic Formula: Use the quadratic formula to solve for the variable.
Example of Solving a Quadratic Equation

| Equation | Solution |
|---|---|
| x^2 + 2x + 1 = 0 | x = -1 |
Polynomials and Rational Expressions

Polynomials are expressions consisting of variables and coefficients combined using addition, subtraction, and multiplication. Rational expressions are expressions in which the numerator and denominator are polynomials. In Algebra 1, you will learn how to work with polynomials and rational expressions.
- Polynomials: Expressions consisting of variables and coefficients combined using addition, subtraction, and multiplication, e.g., 2x^2 + 3x - 1.
- Rational Expressions: Expressions in which the numerator and denominator are polynomials, e.g., (2x^2 + 3x - 1) / (x + 1).
Example of Adding Polynomials

| Polynomials | Sum |
|---|---|
| 2x^2 + 3x - 1, x^2 + 2x + 1 | 3x^2 + 5x |
Conclusion

Algebra 1 is a fundamental course in mathematics that builds upon the concepts learned in elementary and middle school. By mastering the key concepts, formulas, and techniques outlined in this guide, you will be well-prepared to succeed in Algebra 1 and future math courses. Remember to practice regularly and apply the concepts to real-world problems to reinforce your understanding.
What is the main focus of Algebra 1?

+
The main focus of Algebra 1 is to introduce students to variables, equations, and functions, which are essential for problem-solving in various fields, including science, technology, engineering, and mathematics (STEM).
How do I simplify expressions in Algebra 1?

+
To simplify expressions in Algebra 1, you need to apply the order of operations (PEMDAS): parentheses, exponents, multiplication and division, and addition and subtraction.
What is the difference between linear equations and linear inequalities?

+
Linear equations are equations in which the highest power of the variable(s) is 1, while linear inequalities are inequalities in which the highest power of the variable(s) is 1.



